Groundwater Management under Uncertain Seasonal Recharge
After watching the great overview on groundwater resources in California by Thomas Harter (see video above), you will have a better understanding of the issues discussed in this project.
Managing water resources is one of the most pressing environmental challenges of the coming decades. With a changing climate, growing population and change of land use, the stress on water resources has dramatically increased. Whereas policies are emerging on the use of surface water, groundwater is still lacking sustainable exploitation strategies.
Designing optimal policies for groundwater extraction is challenging, particularly because of the uncertainties on the climate, subsurface and human behavior. In this study, we (me and Thomas Hossler) approached a simplified groundwater management problem with the formalism of Markov Decision Processes (MDPs).
Introduction
Optimal groundwater resources management has become crucial over the last decades with changing weather pattern and increased stress on the resource. The risks from suboptimal management are multiple, from saltwater intrusion in coastal aquifer to land subsidence.
The challenge with groundwater resides in the difficulty to gather direct information on the aquifer. Indeed, estimating just the amount of water available or the level of the aquifer is subject to many uncertainties, making the formulation of an adequate policy challenging. The objective of such policy is to maximize the groundwater production to match the needs of the population without any environmental impacts.
There are various uncertainties involved in this decision-making process. The rock permeability that controls the water level, the rainfall that dictates the recharge of the aquifer or the pressure gradient that creates the flux are some of many examples of uncertain variables that play a crucial role in the groundwater usage. Under these conditions, it becomes challenging to optimize the pumping of groundwater over space and time.
Methodology
In this project, we only considered the uncertainty about the rainfall for the upcoming year. We attempted well-established algorithms for sequential decision making, and compared the obtained policies with the global optimal policy found with brute force exploration by assuming full knowledge of the future rain.
Groundwater model
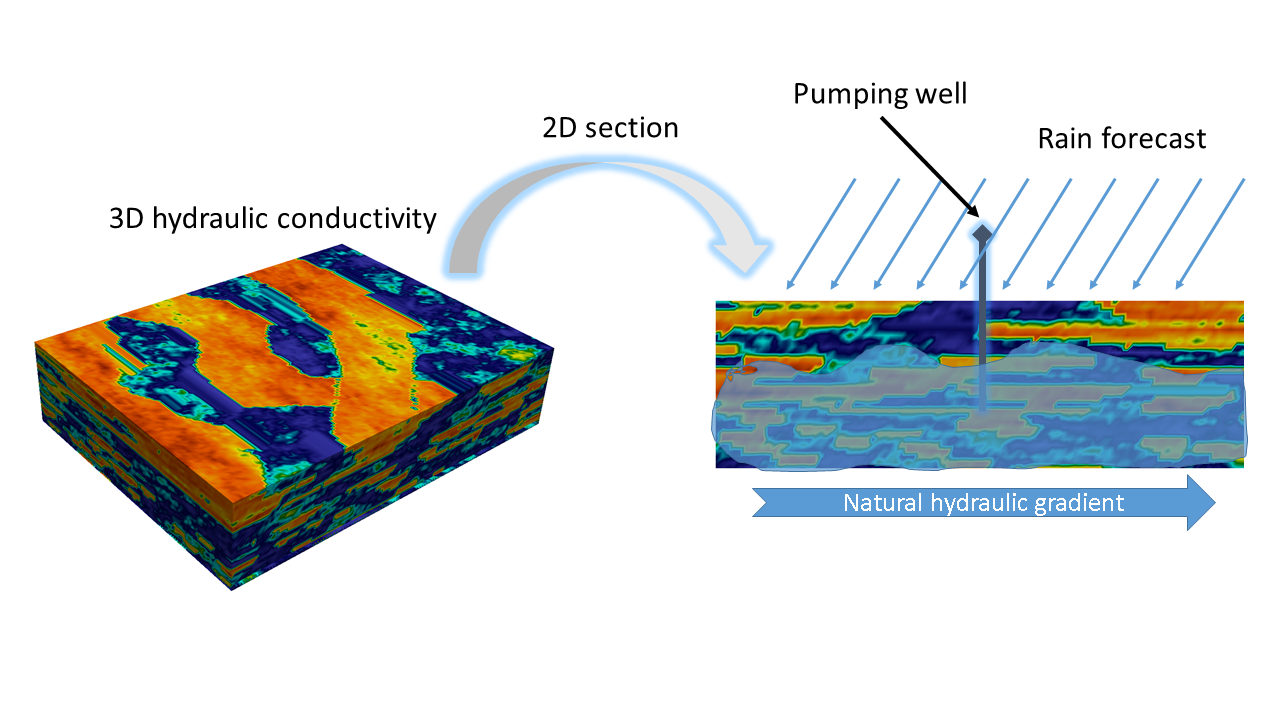
A generative model was implemented using Flopy, a python script of MODFLOW, a 3D finite-difference groundwater simulator developed by the U.S. Geological Survey. The model takes as input a hydraulic head map (i.e. pressure map), a pumping rate, and recharge from the rain, and outputs the hydraulic head after a month of pumping.
The flow dynamics depend on rock properties such as hydraulic conductivity and porosity. These were filled from a vertical section of a 3D model known as Stanford V, illustrated below:
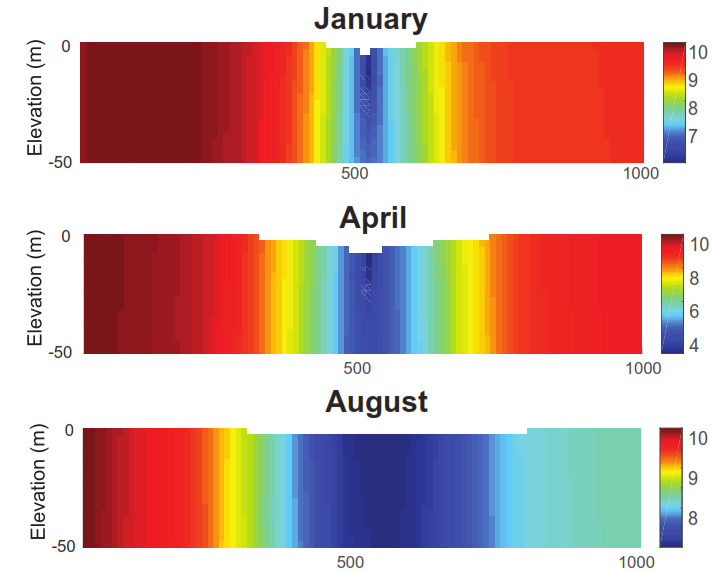
Simple runs of the model with a fixed pumping rate show the cone of depression near the well for different months of the year.
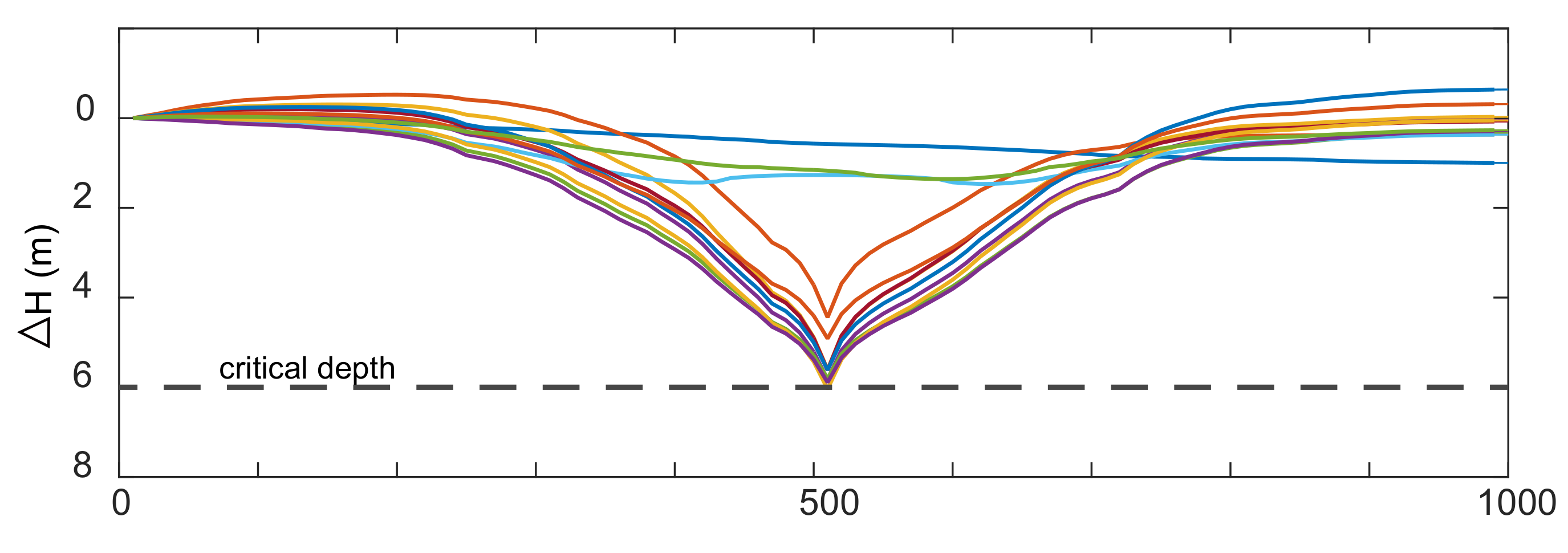
The goal is to pump water from the aquifer in a way that keeps the water table above a certain critical depth:
Formulation of the (PO)MDP
An optimal pumping policy must be chosen that maximizes the profit of a single agent operating under a set of constraints imposed by the government. The agent is allowed to extract water from the aquifer to attend the demand of the local community but it cannot do so if the water table is depleted below a critical depth.
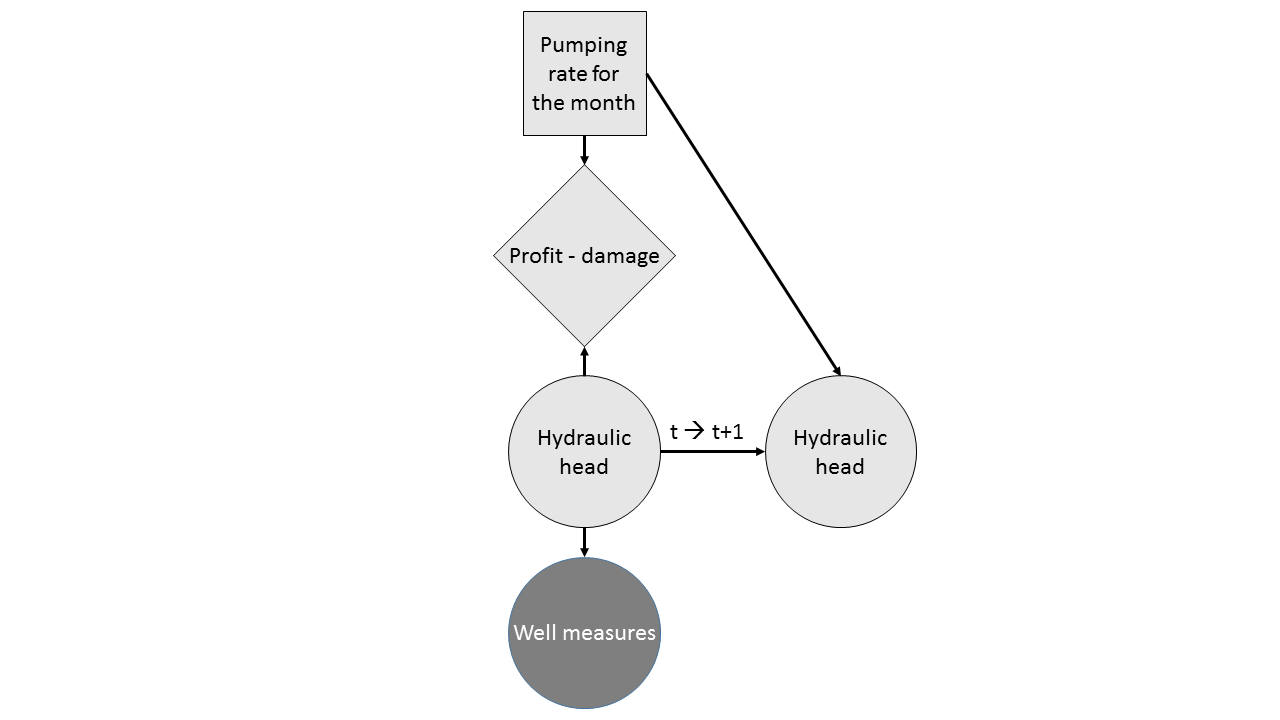
Four pumping rate levels were permitted in the model ranging from no-pumping (\(q_o\)), low pumping (\(q_l\)), mid pumping (\(q_m\)) and high pumping (\(q_h\)). Given our current belief about the state of the aquifer and water table measurements on neighboring observation wells, a decision has to be made about which pumping rate the agent has to commit today without the knowledge of the rainfall in the upcoming months. The decision network for this sequential decision making problem is illustrated below:
We had a very simple reward model accounting for the amount of water extracted and the water table:
\[\text{Reward} = \begin{cases} aV - bV^{2} - cDV & \text{if } D < d_c \\ -100 & \text{otherwise} \end{cases}\]with \(V\) the extracted water volume, \(D\) the depth to water, and \(a\), \(b\), \(c\), \(d_c\) parameters of the model.
Two formulations were considered:
- MDP with unknown transition model
- POMDP where the hydraulic heads are not fully observable
For solving the MDP formulation we used Q-learning, whereas for the more realistic POMDP formulation we used POMCP-DPW with a custom particle filter for updating beliefs on hydraulic maps.
Results
Q-learning
In the plot below, we show the pumping rate level for each month of the year as well as the rain profile, depicted with a solid black line. The pumping policy obtained by Q-learning matched the optimal policy obtained by brute force.
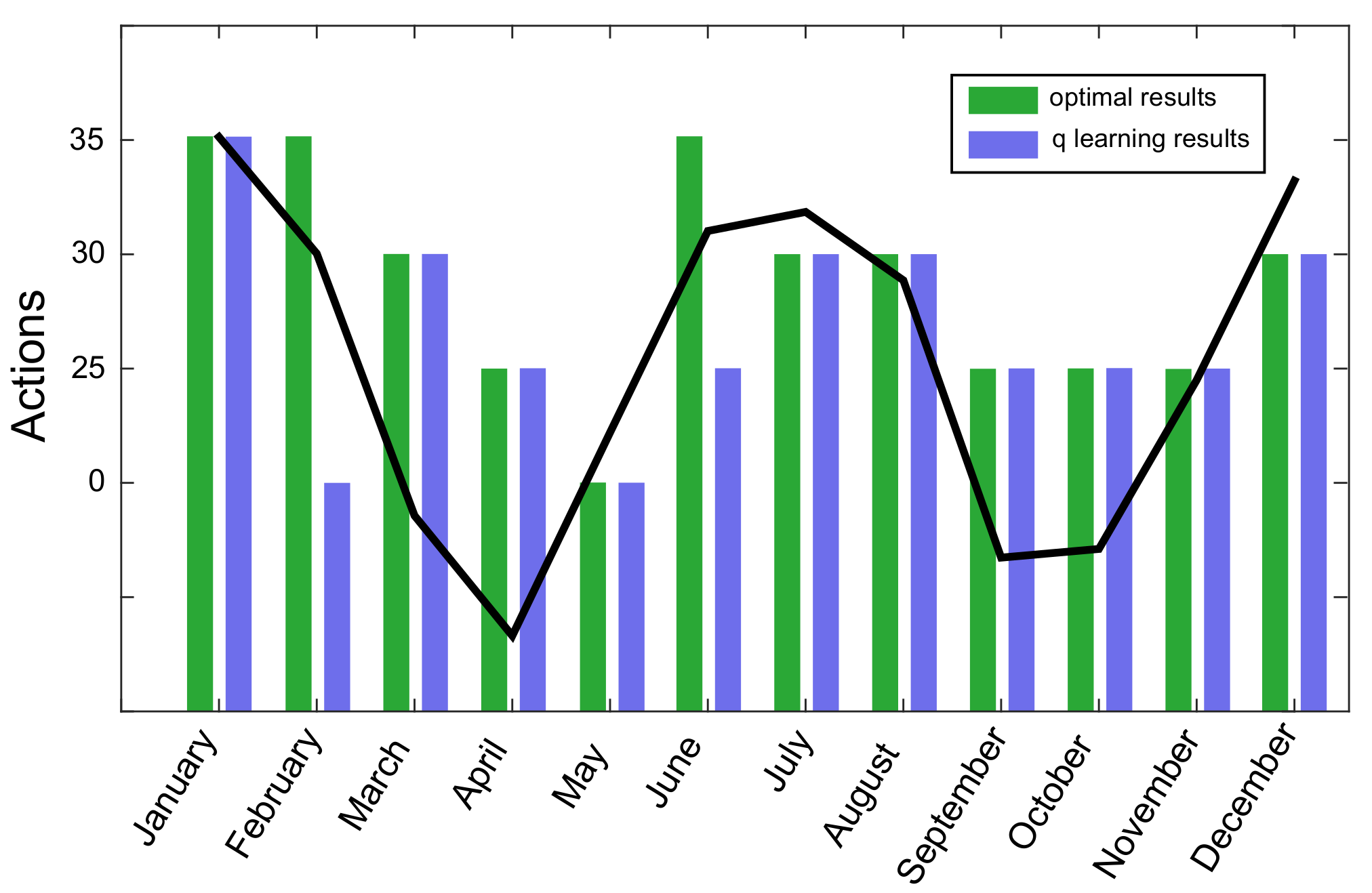
We emphasize, however, that this MDP setup is very unrealistic. In practice, we do not have access to the hydraulic head map in the subsurface. This formulation served to verify the correctness of our implementation.
POMCP-DPW
In the realistic setup in which observations of water table are made at neighboring wells only, POMCP-DPW fails to find a good policy. Although the method is suitable for large state spaces, it has rarely been applied to problems where states are as large as continuous pressure maps.
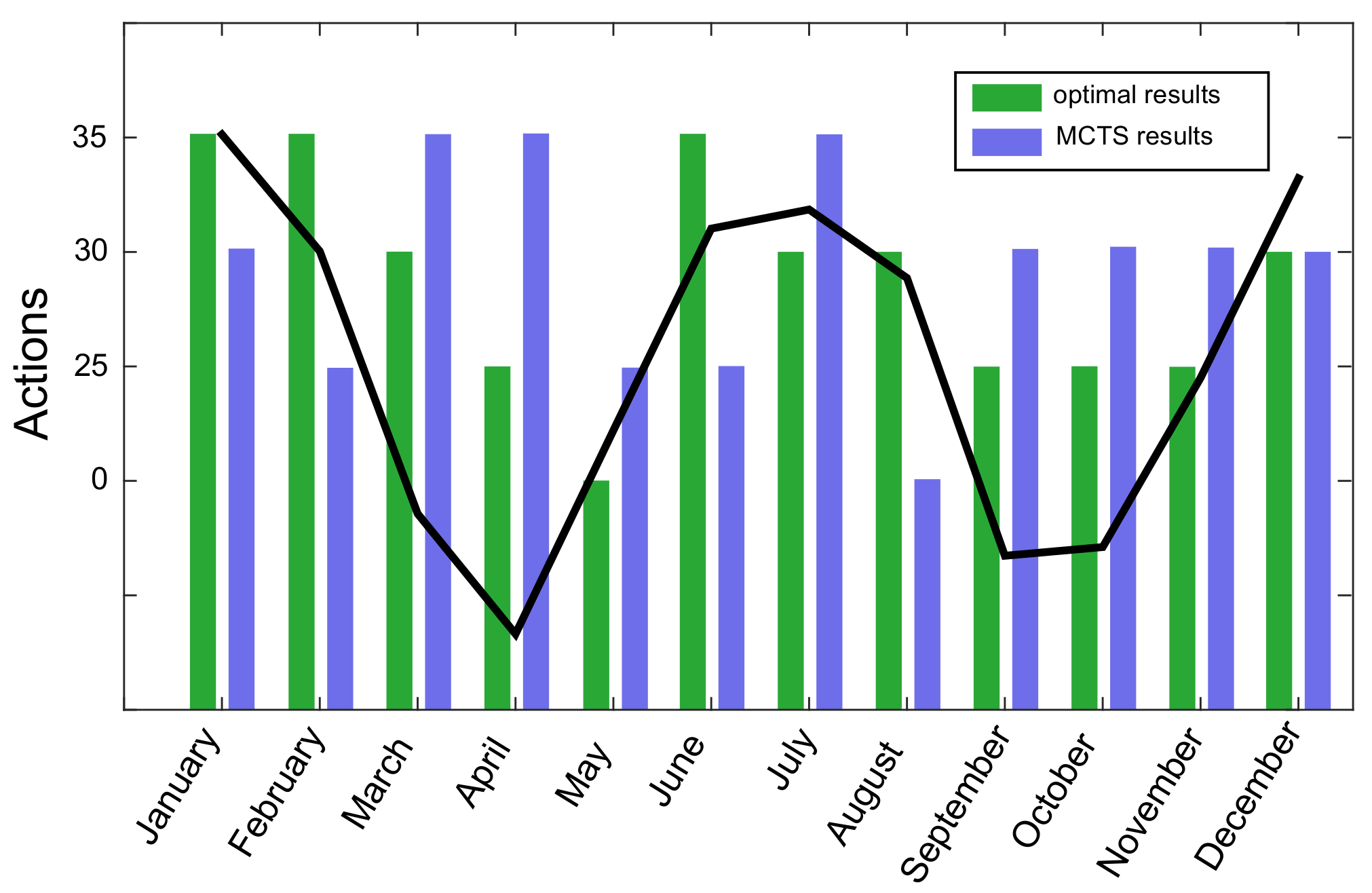
Future collaborations
The problem of managing water/energy resources is relevant to a sustainable future and is also very challenging as demonstrated through this exercise. For future collaborations, I would like to investigate the POMDP methods used in this project more carefully and to include more domain knowledge in the proposed solution.
If you have similar interests or a real dataset (e.g. groundwater, petroleum reservoir) on which we could collaborate, please don’t hesitate to contact me using any of the links on this website.
